实例2：根轨迹绘制

根轨迹绘制的一般步骤：

1. 确定实轴上的根轨迹
2. 确定根轨迹的渐近线
3. 确定分离点
4. 确定起始角与终止角
5. 确定根轨迹与虚轴的交点

  设系统开环传递函数为：
$G(s)H(s) = \frac{K^*}{s(s+3)(s^2+2s+2)}$
试绘制闭环系统的概略根轨迹。

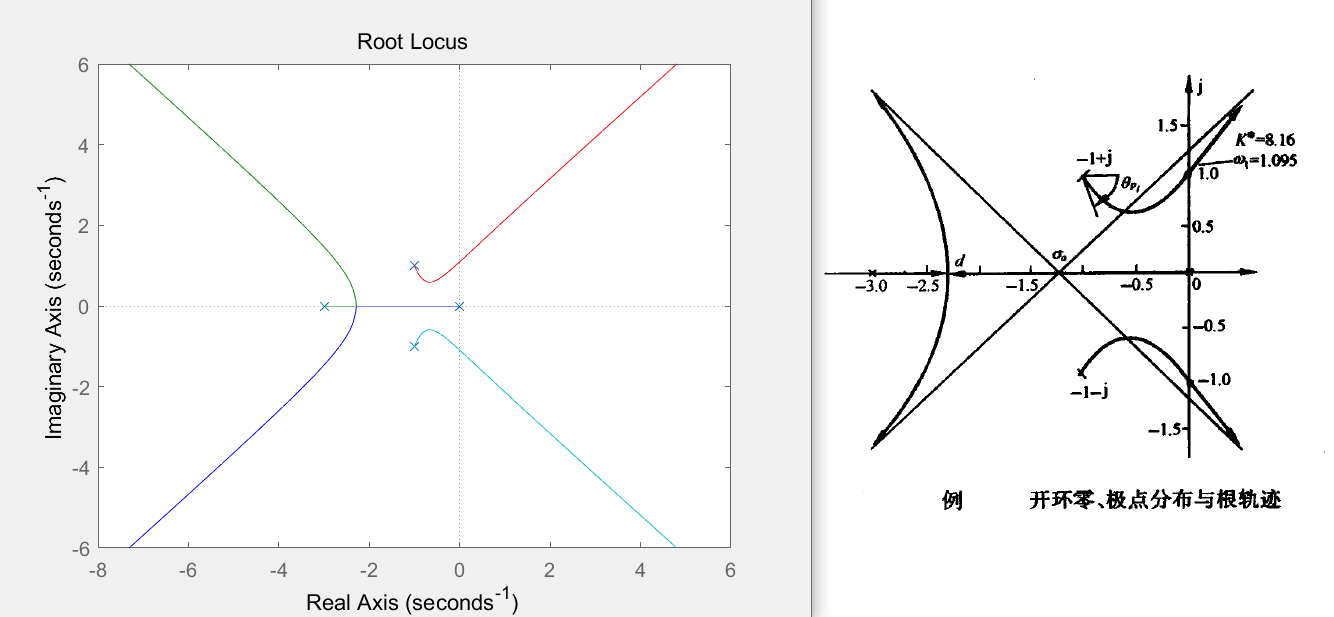
  解： 极点：0 -3 -1+j -1-j
  按下述步骤绘制根轨迹：
  1）确定实轴上的根轨迹。 实轴上 [0,-3] 为根轨迹。
  2）确定根轨迹的渐近线。 由 $n-m=4$ 可知，有4条渐近线，其：
$\sigma_a = \frac{\sum_{i=1}^{4}p_i-0}{4} = \frac{(0-3-1+j-1-j)-0}{4} = -1.25$

$\phi_a = \frac{(2k+1)\pi}{4} = \frac{\pi}{4} , \frac{3\pi}{4} ,\frac{5\pi}{4} , \frac{7\pi}{4}$

  3）确定分离点。 本题没有有限零点，因此

$\sum_{i=1}^n\frac{1}{d-p_i} = 0$

  即

$\frac{1}{d} + \frac{1}{d+3} + \frac{1}{d+1-j} + \frac{1}{d+1+j} = 0$

  解得：$d = -2.2886$ 。

  4）确定起始角（本题无终止角）。

  $s =-1+j$ 时：
  $\theta_1 = \angle(-1+j-0) = \angle(-1+j) = 2.3562$
  $\theta_2 = \angle(-1+j+3) = \angle(2+j) = 0.4636$
  $\theta_3 = \angle(-1+j+1+j) = \angle(2j) = 1.5708$

  由相角条件：$0 - (\theta_0+\theta_1+\theta_2+\theta_3) = (2k+1)\pi$
  得：$\theta_0 = (-2k-1-(2.3562+0.4636+1.5708)/\pi)\pi = (-2k-2.3976)\pi = -0.3976\pi = -71.5680^\circ (k=-1)$

  5）确定根轨迹与虚轴的交点。 本题闭环特征方程式为
$s^4 + 5 s^3 + 8 s^2 + 6 s + K^* = 0$
  令 $s = j\omega$ ，则
$(j\omega)^4 + 5 (j\omega)^3 + 8 (j\omega)^2 + 6 (j\omega) + K^* = 0$
  即
$(\omega^4-8\omega^2+K^*) + j(-5\omega^3+6\omega) = 0$
  解得
$\omega = 0,\pm1.0954$
  其中$\omega=0$不是欲求之解，将$\omega = \pm1.0954$ 代入实部方程，解得 $K^* = 8.1594$ 。

  因此整个系统根轨迹如图：