题目：对于高阶系统的设计问题，往往要进行降阶近似处理，并要验证近似效果。已知某高阶系统模型为:

$G(s) = \frac{194480+422964s+511812s^2+278376s^3+82402s^4+13285s^5+10861s^6+35s^7}{9600+28880s+37492s^2+27470s^3+11870s^4+3017s^5+437s^6+33s^7+s^8}$

经简化处理后，模型等效为:

$G(s) = \frac{d+es}{a+bs+cs^2}$

求a、b、c、d、e，给出选取理由，用Matlab计算并绘图比较两个模型在单位阶跃信号作用下的响应情况，并分析近似效果。

Pade降阶方法

matlab程序如下：

G0t = [35 10861 13285 82402 278376 511812 422964 194480];
G0f = [1 33 437 3017 11870 27470 37492 28880 9600];
G0 = tf(G0t,G0f);
Gp = pademod(G0,1,2);
figure(1)
subplot(1,2,1)
step(G0);hold on
step(Gp); hold off
subplot(1,2,2)
impulse(G0,8);hold on
impulse(Gp,8); hold off
figure(2)
margin(G0);hold on
margin(Gp); hold off

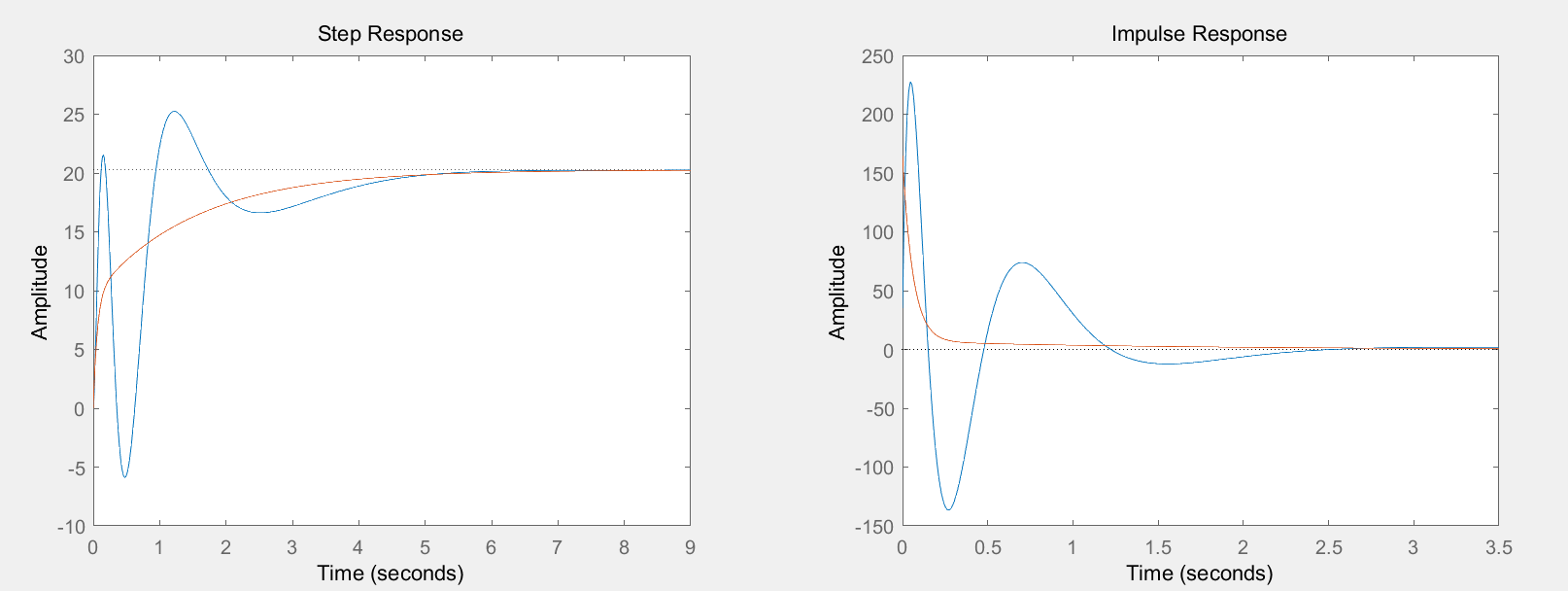
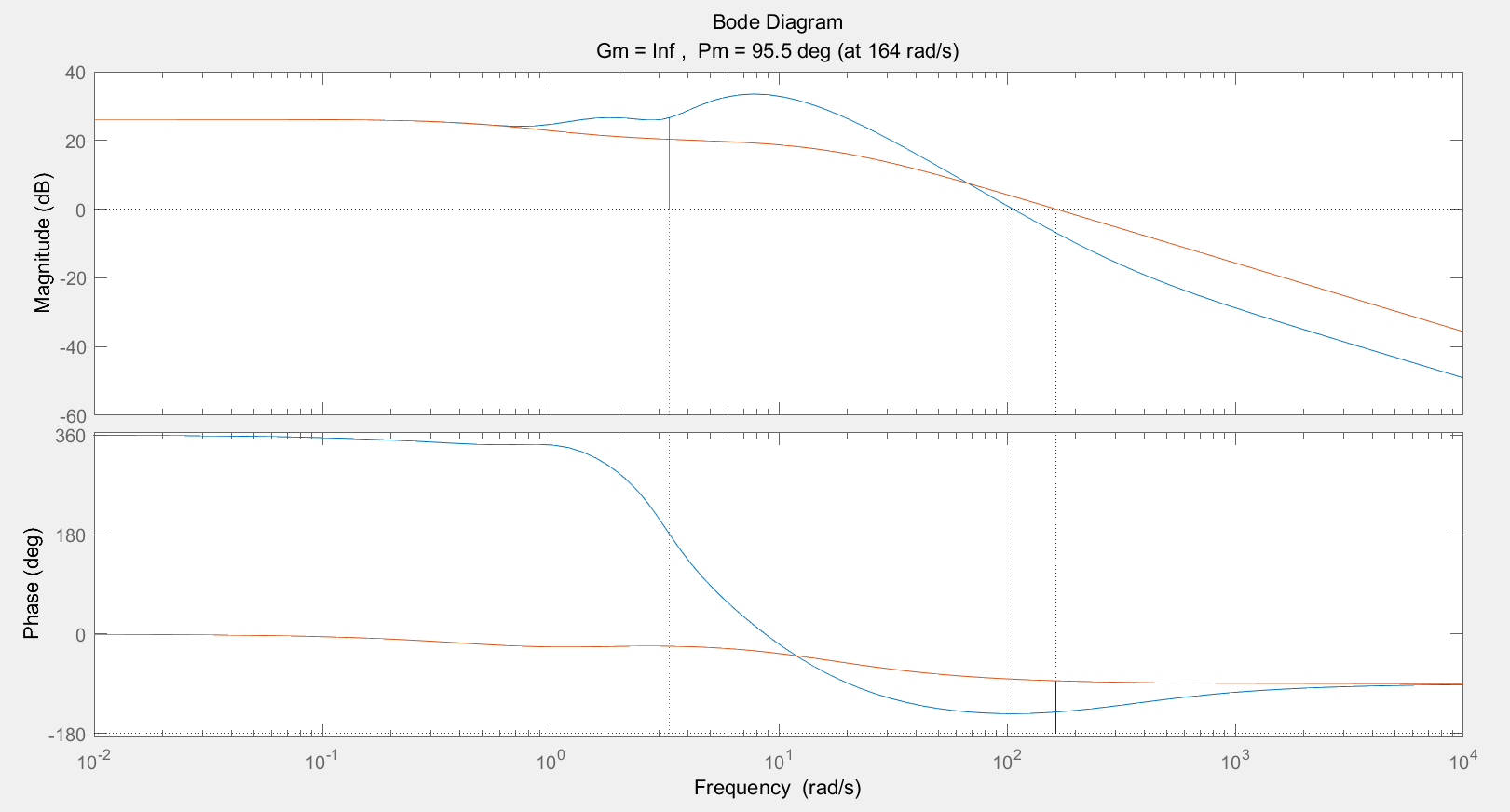
降阶后模型：

>> Gp

Gp =
 
     164.9 s + 217.4
  ---------------------
  s^2 + 17.08 s + 10.73
 
Continuous-time transfer function.

其中，程序中用到的函数如下：

function Gr=pademod(G,r,k)
c=timmomt(G,r+k+1); Gr=pade_app(c,r,k);

function M=timmomt(G,k)
G=ss(G); C=G.c; B=G.b; iA=inv(G.a); iA1=iA; M=zeros(1,k);
for i=1:k, M(i)=-C*iA1*B; iA1=iA*iA1; end

function Gr=pade_app(c,r,k)
w=-c(r+2:r+k+1)'; vv=[c(r+1:-1:1)'; zeros(k-1-r,1)];
W=rot90(hankel(c(r+k:-1:r+1),vv)); V=rot90(hankel(c(r:-1:1)));
x=[1 (W\w)']; dred=x(k+1:-1:1)/x(k+1);
y=[c(1) x(2:r+1)*V'+c(2:r+1)]; nred=y(r+1:-1:1)/x(k+1);
Gr=tf(nred,dred);

Routh 降阶方法

matlab程序如下：

G0t = [35 10861 13285 82402 278376 511812 422964 194480];
G0f = [1 33 437 3017 11870 27470 37492 28880 9600];
G0 = tf(G0t,G0f);
Gr = routhmod(G0,2);
figure(1)
subplot(1,2,1)
step(G0);hold on
step(Gr); hold off
subplot(1,2,2)
impulse(G0,8);hold on
impulse(Gr,8); hold off
figure(2)
margin(G0);hold on
margin(Gr); hold off

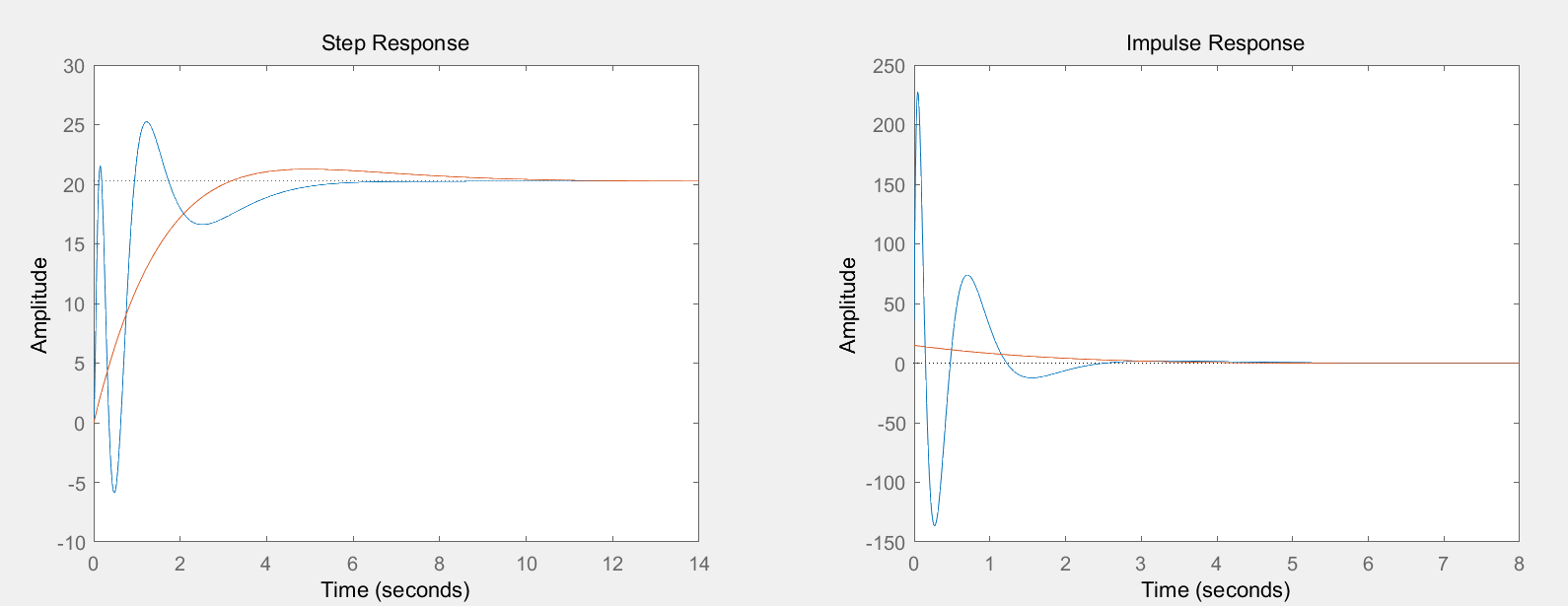
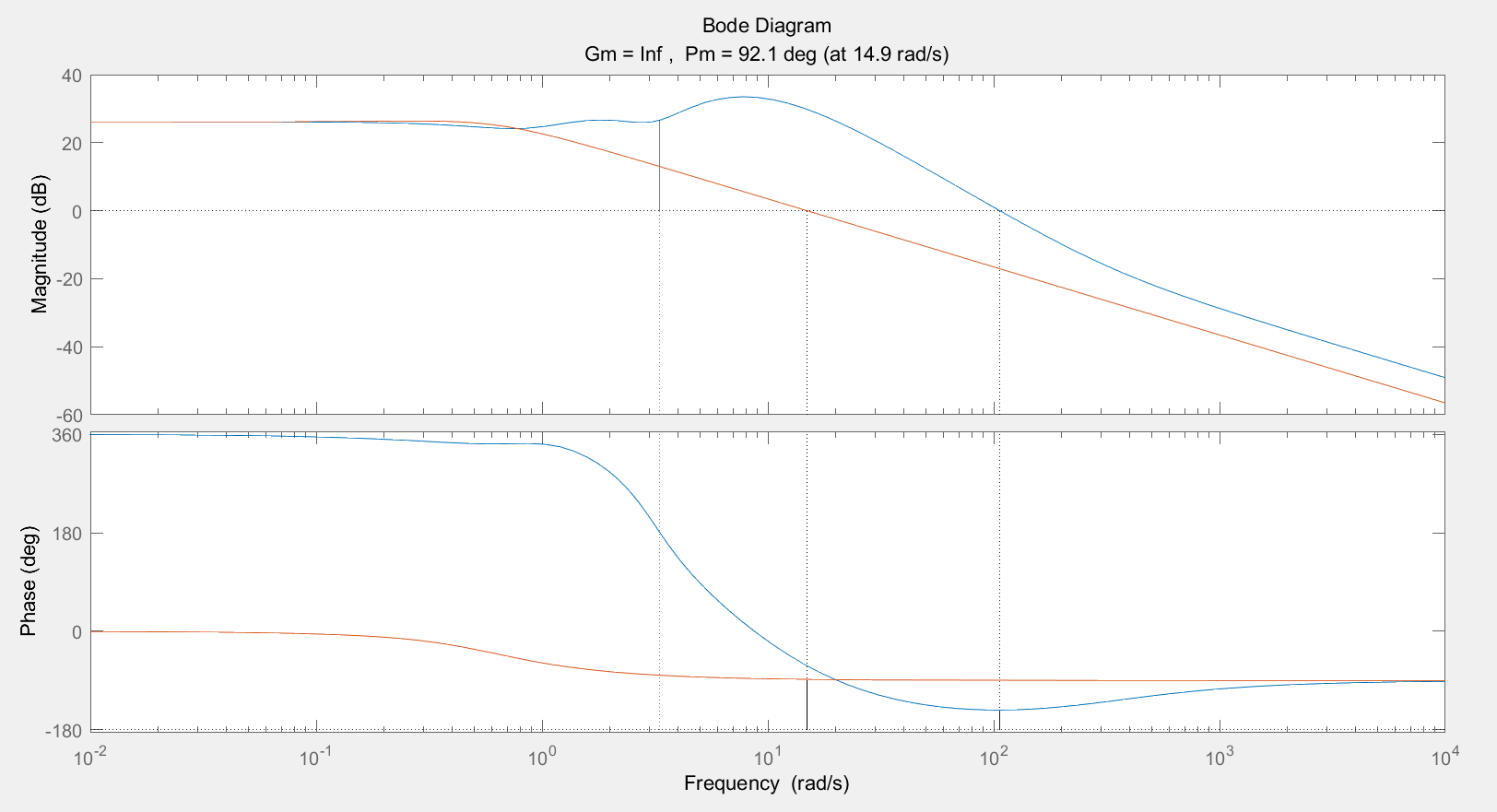
降阶后模型：

>> Gr

Gr =
 
     14.91 s + 6.857
  ----------------------
  s^2 + 1.018 s + 0.3385
 
Continuous-time transfer function.

其中，程序中用到的函数如下：

function Gr=routhmod(G,nr)
num=G.num{1}; den=G.den{1}; n0=length(den); n1=length(num);
a1=den(end:-1:1); b1=[num(end:-1:1) zeros(1,n0-n1-1)];
for k=1:n0-1,
k1=k+2; alpha(k)=a1(k)/a1(k+1); beta(k)=b1(k)/a1(k+1);
for i=k1:2:n0-1,
a1(i)=a1(i)-alpha(k)*a1(i+1); b1(i)=b1(i)-beta(k)*a1(i+1);
end, end
nn=[]; dd=[1]; nn1=beta(1); dd1=[alpha(1),1]; nred=nn1; dred=dd1;
for i=2:nr,
nred=[alpha(i)*nn1, beta(i)]; dred=[alpha(i)*dd1, 0];
n0=length(dd); n1=length(dred); nred=nred+[zeros(1,n1-n0),nn];
dred=dred+[zeros(1,n1-n0),dd];
nn=nn1; dd=dd1; nn1=nred; dd1=dred;
end
Gr=tf(nred(nr:-1:1),dred(end:-1:1));